== Nopelepsy technical introduction === Talking about a way detect possible epilepsy-sensitive flashes in videos.
EDIT(2020-06-05): This post references an older post I made to my previous website which I ended up taking down. Nothing in the older post is necessary to understand this one.
In my last post a little under two years ago, I talked about a theoretical way to tackle the problem of removing flashes from video, specifically those that can cause epileptic events. Due to technical limitations, time, and scope change, this project has changed a lot over that time. A couple months ago I stopped stalling and buckled down to actually built a working version of the damn thing. It took a lot of trial and error, false starts, and good old fashioned procrastination, but I have a working copy now call Nopelepsy. (It’s in closed alpha at the time of writing, but you want a copy, email me. My contact info is at the bottom of the page). This is my attempt at writing up what I’ve done so far, from ideas to implementation to pitfalls.
EDIT(2020-06-05): I referenced “closed alpha,” but at the time I neither had any idea about what that actually meant, nor did I have anyone contact me.
Last time I wrote about this, I was trying to read directly off of the visible screen and preemptively block out areas of the screen that might flash too many times in too short of a period. The idea was that you wouldn’t have to download YouTube videos and run them through a converter in order to watch YouTube videos, or do something similar for gifs on the internet. It would be a one-time thing, just run it and be protected while on your computer. There was one little problem, though.
This was slow.
Like, way too slow, and it’s not the kind of slow that can be sped up easily either. Nopelepsy needed to be fast enough to detect flashes that are at least 1/30th of a second, and there was no way that method was going to be getting those kinds of benchmarks. Also, during that time I figured that I should also support detection for people who are photosensitive in general, but that would be impossible without having some access to future information on the screen.
So I eventually decided, instead of making a shitty screen reader system, to make a video converter and make it good. This way I can have access to future information about the screen, and can theoretically have perfect flash detection.
This is how the current version of Nopelepsy works. It takes in a video file (like a movie or something), processes it, and then spits out a different video file with all of the light flashes gone. The techniques are in their infancy, but they work. Here are some videos of it in action:
Warning: To my knowledge these videos do not contain any harmful flashes, but they might. Some of these clips were initially flash-heavy before being ran through the converter, so some flashing may have gotten through.
The method I currently use to detect and remove flashes has had a checkered past. Here I’m going to try to describe what I do to get the results that I do, and also some of what doesn’t work. First though, we need to get some objectives and definitions out of the way. All of these are inspired or come straight from link(https://www.w3.org/WAI/GL/WCAG20/#general-thresholddef)[the W3C accessibility spec].
Def. Potential flash: An increase followed by a decrease in the luminance of a pixel of at least 1/10th the maximum sRGB luminance. These are defined by the pixel location and the range of time that this takes place.
The dependence on sRGB luminance instead of some other color space shouldn’t be necessary, but it’s what the spec uses so I’m going to stick with that for now. The range of time that a potential flash is happening over will be called its domain. Also note that potential flashes can overlap and can nest inside each other.
img(potential.jpg)[]
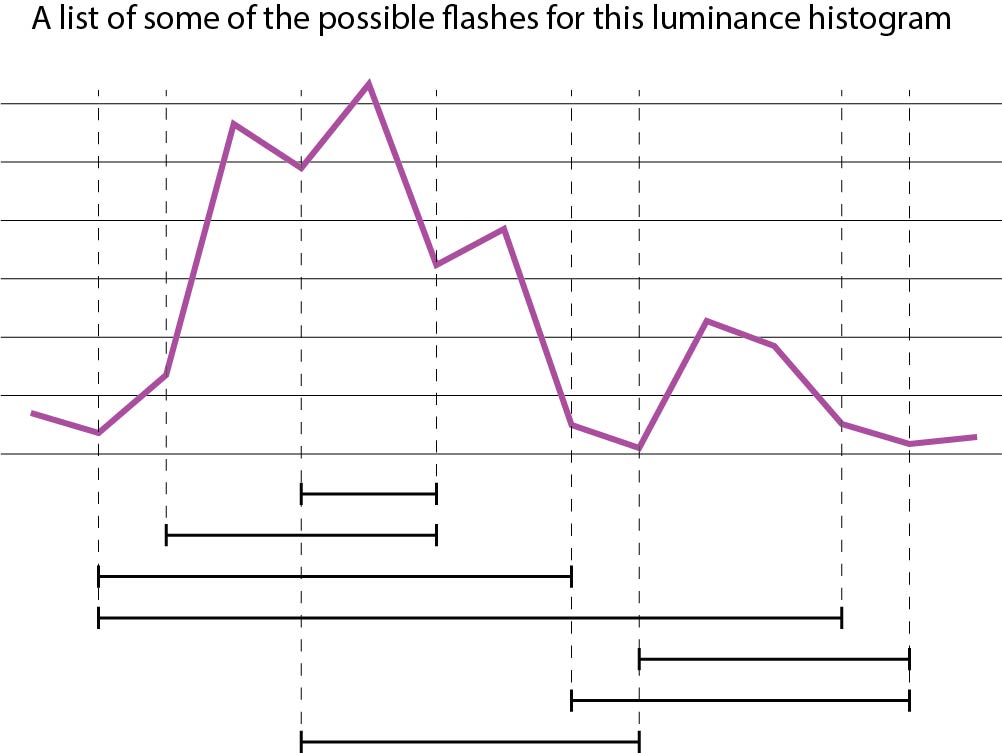
Def. General flash: When 25% or more of the pixels inside of any 0.024 steradian region (relative to the viewer) all experience a potential flash concurrently.
This definition comes (modified) from the W3C spec. It’s rather ambiguous as to what it means by “concurrently” and “region”, so I’m setting some additional guidelines to make the problem more defined and also a bit easier:
Now to take care of the “concurrently” problem. Depending on how you define it, you can have a mess on your hands. For example, say pixels A, B, and C all have potential flashes, named $p_A$, $p_B$, and $p_C$, respectively. Now also assume that $p_A$ flashes concurrently with $p_B$, and that $p_B$ flashes concurrently with $p_C$. Now is it necessarily true that $p_A$ and $p_C$ flash concurrently as well? How you answer this affects how you solve the problem.
In Nopelepsy, we assume that yes, it’s necessarily true that $p_A$ and $p_C$ must also flash concurrently. Denote $\sim$ to be a relation and $p_X \sim p_Y$ to mean “$p_X$ and $p_Y$ flash concurrently.” Now obviously $p_X \sim p_X$ for any potential flash $p_X$. The word “concurrent” also implies that if $p_X \sim p_Y$, then $p_Y \sim p_X$ as well. If we add on the assumption that that we just talked about, then we know that $\sim$ is transitive, and so $\sim$ is an equivalence relation.
From undergrad math we know that equivalence relations are exactly the same as partitions, and so we now have an efficient way of testing all potential flashes against every other potential flash: just test each again any one member of each of the partitions.
That’s all well and good, but what exactly is the relation? The thing is… I don’t know. It’s one of those things that I know when I see it, and I can point them out in concrete examples, but I can’t give you a straight defintion. In any such definition, we want to not only capture the fact that the potential flashes are happening at the same time, but also that they have the same “shape.” Here are some illustrations in which the former succeeds and the latter fails.
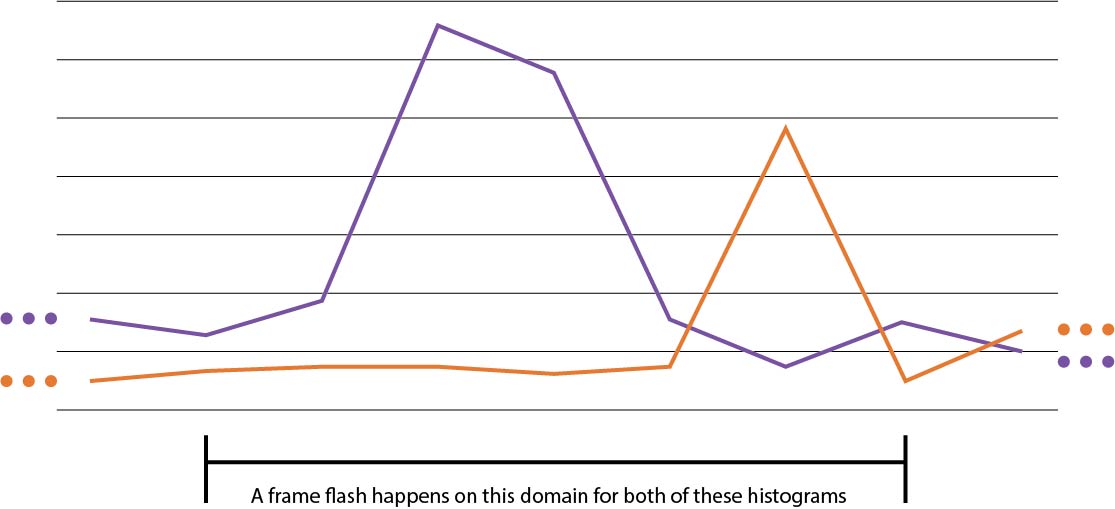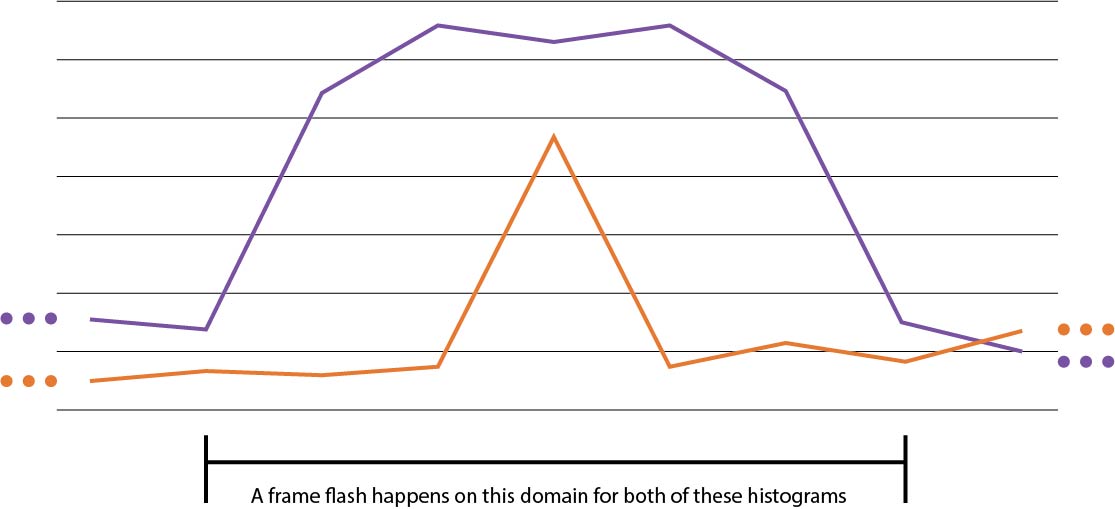Why is this a problem? Well we not only want to remove all flashes, but we also want to not detect as much non-flashing stuff as possible. One major goal is to be as non-disruptive to the movie as possible, and that can’t happen when two cars driving next to each other is enough to trigger the detector. However, I also don’t know exactly what the relation should be, so I’ve decided to instead try to Frankenstein together a robust solution from various non-robust ones.
Let $\sim$ and $\sim’$ be two different ways of interpreting “concurrent” from the above discussion. Now let $\approx$ be another relation such that $p_X \sim p_Y$ and $p_X \sim’ p_Y \iff p_X \approx p_Y$. Then $\approx$ is also an equivalence relation. So the idea is to come up with many of these relations that all do a good job at grouping together the potential flashes that are actually concurrent and then “multiplying” them all together like this!
img(multiplication.jpg)[]
So now the question comes down to: what are some good candidates? I’m going to give the two that Nopelepsy has implemented and give some arguments as to why I think these are good candidates.
Domain equality: if $[a, b]$ and $[c, d]$ are the domains of 2 potential flashes, the Domain Equality $\sim$ says they flash concurrently if and only if $a = c$ and $b = d$. Some reasoning behind this:
Center of Mass equality: Let $[a, b]$ and $[c, d]$ be as before, and also let $\left( p_{i} \right)$ and $\left( q_{i} \right)$ be the luminance histograms of the two potential flashes, respectively. Denote
\[P = \left[ \sum_{i=a}^{b} \frac{i p_i}{\sum p_j} \right], Q = \left[ \sum_{i=c}^{d} \frac{i q_i}{\sum q_j} \right]\], where $[ \cdot ]$ means “nearest integer, rounding up at 0.5, etc.” The Center of Mass $\sim$ is satisfied if and only if $P = Q$. This is meant to quantify a bit about the “shape” of the luminance graph. It’s rather crude, and that’s why it’s still tagged “EXPERIMENTAL” in Nopelepsy, but it seems to work just fine…
Now that we’ve gone over what potential flashes are and how we group them together, let’s look at the final algorithm as used by Nopelepsy at the time of writing. The input is a video file, along with some options and preferences, and the output is another “corrected” video file.
Nopelepsy uses a streaming algorithm, so some of the results from the last iteration are piped back into detector again in the next iteration. The whole thing looks like this:
S := queue of video frames
pre-fill S with one second of black frames
for each frame in the video
push the current frame onto S
do the detection and modification directly to the frames in S
if S has a finished frame ready to write to disk
write that file
pop the front off of S
Why is it set up like this? Well, it’s mostly a gut instinct thing. Nopelepsy needs to have access to the luminance histogram, but I can’t load the entire thing into memory. A general flash can happen in literally any chunk of time, so there’s no good way of chopping up video for analysis. As to why I can’t jump multiple frames at a time, I explain why in a couple paragraphs.
Needless to say, the “do the detection” part is the interesting one. The way this happens goes something like this:
function detectAndModify()
F := empty list of potential flash "ballots"
for every pixel in the video dimensions
look at its histogram and determine all potential flashes that could happen
for every potential detected flash
if it flashes concurrently with some potential flash in F, let that pixel "vote" on that flash in F
if not, create a new "ballot", vote on it, and then add it to F
optionally reduce F by looking at its neighbors
for every potential flash ballot in F
for every voter on that ballot
check to see if there are enough other voters around it (25% of the 0.024 steradian region around it)
if not, continue
there is now determined to be a general flash that corresponds to some domain of the voter pixel (the necessary information is all on the ballot)
modify the necessary frames of that voter to get rid of it
Hopefully now it’s clear why we needed all that stuff about equivalence relations. In order to efficiently see if there are enough concurrent potential flashes in the area, we create buckets of potential flashes that are all concurrently flashing with each other. We can then determine which potential flashes from each bucket are actually part of a general flash by looking for neighboring items in that same bucket.
However, it’s not as clean as this. This is actually pretty slow, it’s $O(w h n^2)$ for each iteration, where w,h are the dimensions of the image and n is the number of frames per second of the video (with some optimizations described below it’s actually $O(w h n)$ ). In order to make this faster, Nopelepsy first resizes each frame to some amount decided on by the user. The user enters one of the available pixel block sizes (16x16, 32x32, or 64x64 currently) and then pixel blocks of those sizes get reduced down to a single pixel in the detection image. When a general flash is detected in the histogram of this detection image, both the original frames and the these new ones are modified too keep them in sync.
There’s one more ambiguity that needs to be addressed still. It’s not that hard to come up with a scenario in which more than 25% of the pixels in some neighborhood have potential flashes that agree with one in the center of the region, but for nearly none of them to have that same property. This is especially easy when the resizing (from the previous paragraph) is very aggressive. So the step between the detection and modification is to reduce the voters in each of the ballots in F so that each potential flash is surrounded enough other potential flashes, each of which are surrounded by enough in turn. This may seem like a lot of work, but it makes it so that more aggressive resizes of the video frames still look smooth in the final output, which means we can resize even more and speed up computation.
As one last optimization, we can note that if we’re using the Domain Equality flash criteria from above, and since the algorithm is progressive, we can make use of previous information. Let $B_i$ be the set of all potential flashes whose domain ends on the $i^{th}$ frame in the queue, let $n$ be the number of frames in the queue (remember, the queue is set to a fixed size), and let $\sim$ be any concurrency criteria that is multiplicatively combined with Domain Equality (as described in the previous section). So, for any $a \in B_i$ and $b \in B_j$, we have that $a \sim b \implies i = j$, and so by the contrapositive it’s useless to compare potential flashes between different sets $B_i$ and $B_j$.
Also note that, if no modification happens between this frame and the last, $B_{n}$ last frame is exactly equal to $B_{n-1}$ this frame. If we also assume that, on every frame of the algorithm, all general flashes are removed, then it suffices to just look at the elements in $B_n$ and not worry about the potential flashes in all the other $B_i$ s, because it’s just wasted computation. This is because any general flash with domain ending in any other frame $k \neq n$ would have been made up of potential flashes in $B_k$, and so would have been taken care of $n - k$ frames ago. So, this brings the algorithm from $O(w h n^2)$ to $O(w h n)$.
There are some minor details missing still, like what happens around the corners, how do you juggle luminance and color images, etc, but those are all minor implementation details. I think I’ve described my methods in enough detail that someone else can go behind me and point out all the things I did wrong (which I mean, why else do we write dev blogs in the first place?).
Development isn’t finished yet though! There are still plans for the future. Some of these include:
Anyways, I think that just about wraps up what I had to say about the current stable version of Nopelepsy. Next time I’m going to be dealing with most subtle problems with the detector and brainstorming how to fix it.
Thanks for reading!