== A self-exploration of image compression === A random walk through idea-space will reach enlightenment at a rate of sqrt(2 * n * log log n).
This is an experiment in a different format. This is me documenting my trial-and-error process of learning about image compression. I’m calling this a self-exploration because I’m not going to do any research at all, it’s all going to be guided by my own observations and ideas. All I’m starting off with is an understanding of entropy and arithmetic encoding.
I’ve written a PNG decoder and a zip DEFLATE decoder on two separate occasions, one of which was used for the PNG decoding. This is to say that I know basically nothing about image compression.
Starting out, I’m mostly interested in byte-based compression, not bit-based. I’m also only going to be working with the luminance channel for now. Each image is 1024x1024, so we’re looking at 8388608 bits with no compression. I’m mostly interested in compression and transformations that can be done in parallel via SIMD or GPGPUs easily, and computations that can be done using u8 arithmetic, or arithmetic on Z/256Z. I’m also mostly interested in lossless compression.
Here are the 3 images I’m going to be using. I chose to use images I screencap’d from Shadertoy because they’re visually interesting 3d scenes that I can be absolutely sure have no lossy compression artifacts already.
img3(iq.png)iq.pngsquiggles.png[xp_pipes.png]
For those in the back who have trouble hearing me, I’ll speak up.
YES, I KNOW. A SAMPLE SET OF 3 IMAGES ISN’T REPRESENTATIVE OF IMAGE COMPRESSION AS A WHOLE. THIS IS A VERY SMALL TEST OF VERY SIMPLE TECHNIQUES, AND AN EXCERCISE IS STRENGTHENING MY INTUITION ABOUT COMPRESSION. NOTHING MORE.
Finding the histogram and the entropy of the pixels in the images gives:
Which means that, if I was to just concat the pixel histogram with the arithmetically coded pixel values (assuming that the histogram could be represented in 8 bits per bin without loss of efficiency) we’d get 8071460, 7843458, 7620743 resp, achieving 0.96, 0.93, 0.91 percent file sizes with just that step. Zip files will sometimes contain embedded (themselves compressed) huffman tables, so this isn’t that weird.
Here are the histograms:
img3(iq_base_histogram.png)base histogram iqbase histogram squiggles[base histogram xp_pipes]
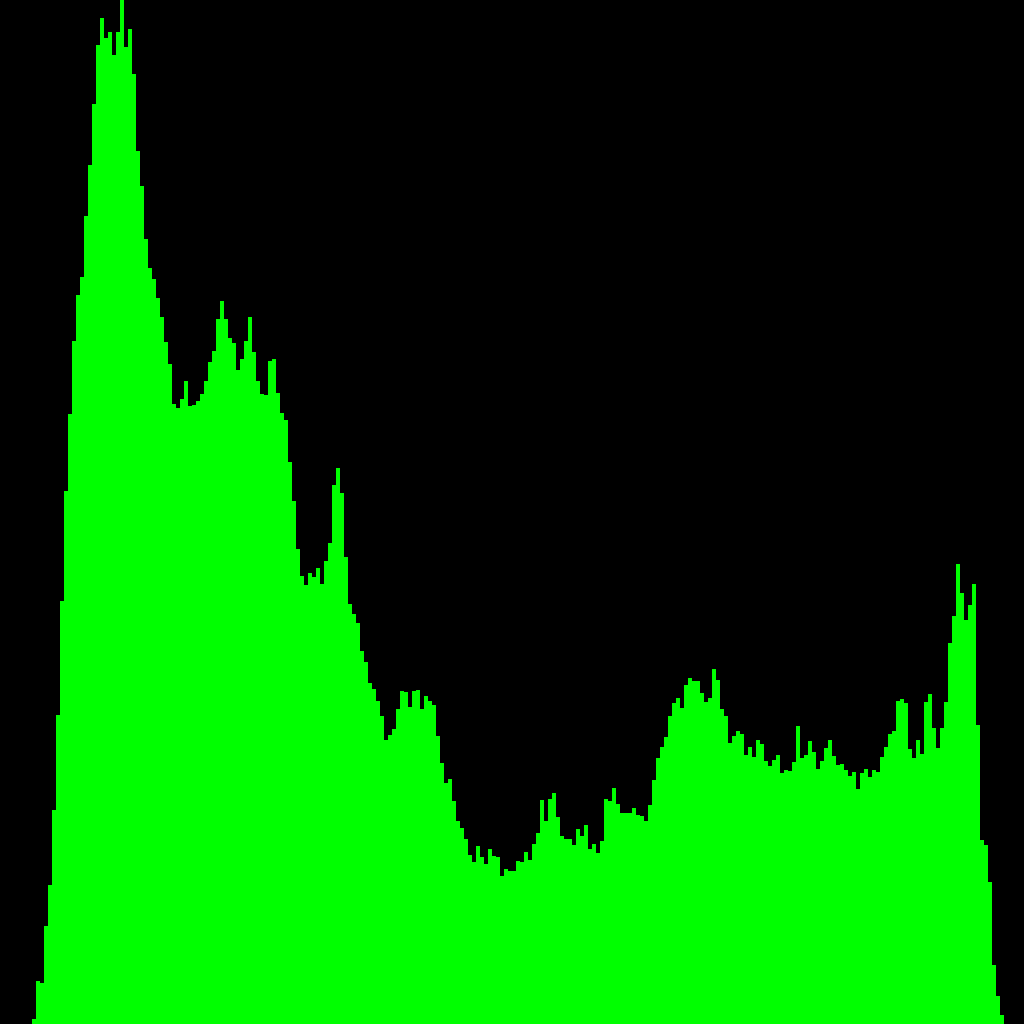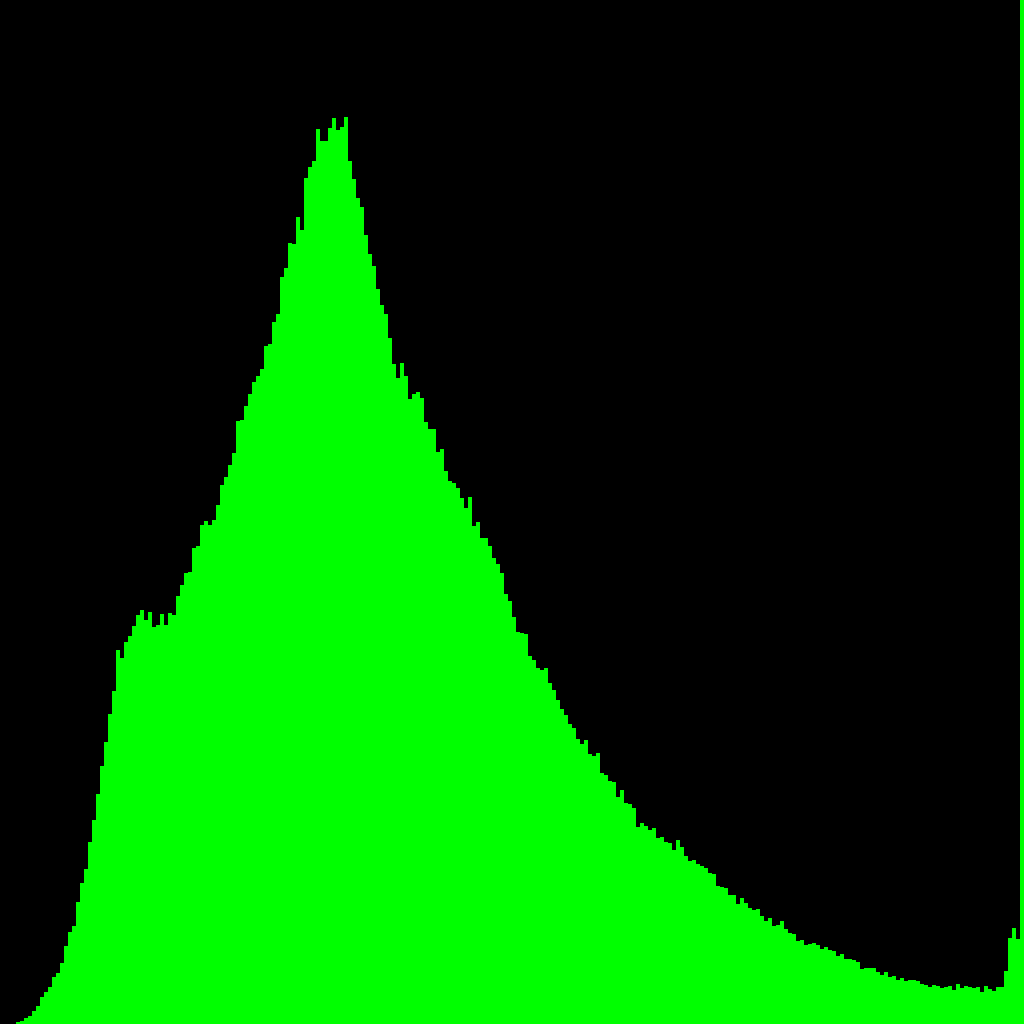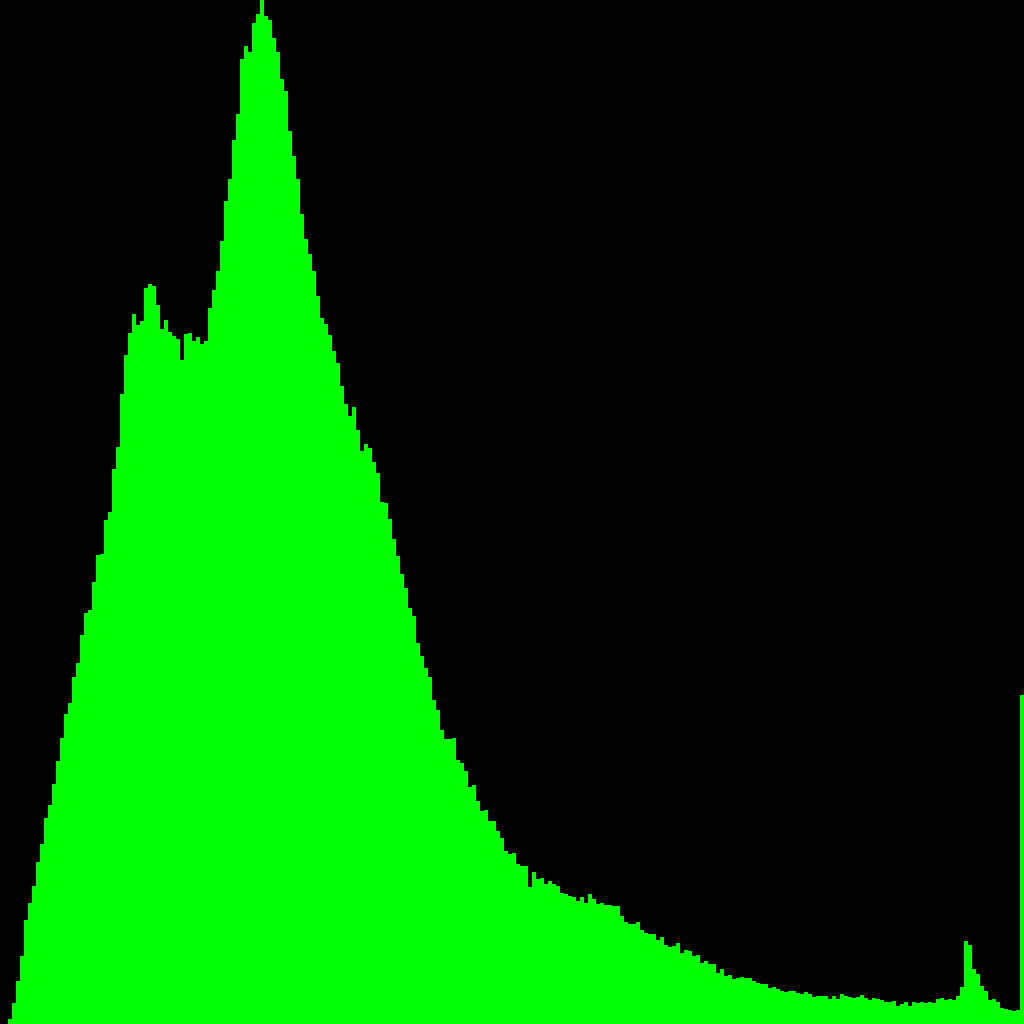Now the basis of all of the image and video compression techniques I know about is that pixels nearby are more similar than pixels far away. I wonder how true that is? Let’s graph pairs of adjacent pixels.
// pairs entropy
int histo[256][256] = {0};
for (int i = 0; i < width*height; i += 2) {
histo[data[i]][data[i+1]] += 1;
}
double entropy = 0;
int max_histo = 0;
for (int p = 0; p < 256; ++p)
for (int i = 0; i < 256; ++i) {
if (histo[i][p] > 0) entropy += histo[i][p] * -log2((double)histo[i][p] / (width*height/2));
if (histo[i][p] > max_histo) max_histo = histo[i][p];
}
printf("entropy: %f\n", entropy);
u8 *out_img = malloc(1024*1024*3);
memset(out_img, 0, 1024*1024*3);
FILE *fout = fopen("out.ppm", "wb");
fprintf(fout, "P6\n1024 1024 255\n");
for (int py = 0; py < 256; ++py)
for (int px = 0; px < 256; ++px) {
double f = (double)histo[px][py] / (max_histo);
int bar_x = px*4;
int bar_y = py*4;
for (int y = bar_y; y < bar_y+4; ++y)
for (int x = bar_x; x < bar_x+4; ++x) {
out_img[(y*1024 + x)*3 + 0] = 0x00;
out_img[(y*1024 + x)*3 + 1] = 0xff*f;
out_img[(y*1024 + x)*3 + 2] = 0x00;
}
}
fwrite(out_img, 1, 1024*1024*3, fout);
img3(iq_pairs_histogram.png)pairs histogram iqpairs histogram squiggles[pairs histogram xp_pipes]
Huh, well that’s pretty conclusive, I’d say. The middle and last are hard to see because there are a couple small areas of pixels that are saturated to white. They’re fairly small, but there’s enough area to them that they totally dominate the histogram. Just for giggles, here’s the the same histograms, but where every bin stores that bin’s entropy.
img3(iq_pairs_entropy_histogram.png)pairs entropy histogram iqpairs entropy histogram squiggles[pairs entropy histogram xp_pipes]
That code snippet also calculates the entropy of entire pixel pairs:
This is pretty nice. Doing the same as last time, encoding pairs of bytes and storing them along with the pairs-of-bytes-histogram, isn’t that bad as of yet, it’s still a win. But it won’t be when we go up to quads of pixels, since the table is now 256*256*8=524288 bits, or 64KB. The one-dimensional histogram, for reference, was 256B. For quads of pixels, the histogram would be 4GB. We’ll get back to that later.
But we’re not there yet. So what would happen if I just transformed every pixel into the difference between it and its neighbor? That’s still a reversible transformation.
// running difference
for (int y = height-1; y >= 1; y -= 1) {
for (int x = 0; x < width; ++x) {
data[y*width + x] = (data[y*width + x] - data[(y-1)*width + x]);
}
}
for (int x = width-1; x >= 1; x -= 1) {
data[x+1] = (data[x+1] - data[x]);
}
int histo[256] = {0};
for (int i = 0; i < width*height; i += 1) {
histo[data[i]] += 1;
}
double entropy = {0};
for (int i = 0; i < 256; ++i) {
if (histo[i] > 0) entropy += histo[i] * -log2((double)histo[i] / (width*height));
}
printf("entropy: %f\n", entropy);
This code, from the bottom up, computes for each pixel the difference between it and the pixel immediately above it. For the top line it computes differences between each pixel and the one to its left. This is a brain-dead simple to decompress in SIMD, so that’s a big win in my book.
Great! File sizes are nearly half the raw uncompressed size for iq.png, and around 70% for the other two. For reference, these single-channel pngs are sized 3652640, 5197448, 5140888 bits resp. So this very simple encoding is within 5% of PNG’s size, measured against the raw entropy compression of the image bytes, or about 10% measured against the PNG sizes. This isn’t representative by any measure, but it is interesting.
No doubt this can be fiddled with, adding bits here or there to pick a better pixel to compare against. But as it stands this compressor is only taking into account one neighbor for each pixel, not a representation of what all of the other pixels around them look like as a whole. So for instance, saying “this block of 16x16 pixels are all smoothly transitioning colors from here to here” will probably be better than “encode a value of -1 for each pixel in this 16x16 block”. This is probably a good direction to go in, I’d imagine. I mean, macroblock coding has to be popular for a good reason, right?
I want to go back to the pixel pairs for a second. Let’s do the transformation data[i+0], data[i+1] -> data[i+0], (data[i+1] - data[i+0]). Taking the entropy of these pairs gives 5903458, 6643549, 6353101. This is exactly the entropy for the pairs untransformed, which is a good sanity check since that transformation is reversible. But just for shits and giggles, what would happen if I were to entropy encode every other byte separately?
// pairs separated
for (int i = 0; i < width*height; i += 2) {
data[i+1] = (data[i+1] - data[i]);
}
int histo[256][2] = {0};
for (int i = 0; i < width*height; i += 1) {
histo[data[i]][i%2] += 1;
}
double entropy[2] = {0};
for (int p = 0; p < 2; ++p)
for (int i = 0; i < 256; ++i) {
if (histo[i][p] > 0) entropy[p] += histo[i][p] * -log2((double)histo[i][p] / (width*height/2));
}
printf("entropy: %f %f = %f\n", entropy[0], entropy[1], entropy[0] + entropy[1]);
Woahhh. I have to admit, I didn’t expect that. I expected the result to be far closer to the original base entropy result. But, thinking about it a little, it makes some sense. Say I’m taking an input of 1 1 2 2 1 1 2 2 and turning it into 1 0 2 0 1 0 2 0. The entropy of adjacent pairs doesn’t change because there’s just as many 1 1s in the first as there are 1 0s in the second, etc. But the entropy of the pairs separated is less than the base entropy because we’re going from an entropy of 4*0.5*log(0.5) + 4*0.5*log(0.5) = 8 to (2*0.5*log(0.5) + 2*0.5*log(0.5)) + 4*1*log(1) = 4.
In addition to the entropy win, there’s also a win in the amount of histogram bits that will have to go in the file too. As said previously, at 8 bits per bucket of the pixel pairs histogram (at the moment I’m only thinking about storing the histograms uncompressed), we’re looking at 64KB. With this method we’re looking at a histogram size of 512B.
But the win I’m most interested in is the following: we have a very cheap and expandable method of generating distributions that have decent entropy, and a lower bound on the best entropy that this method is able to achieve. Because this pair separation method will never be able to get a lower entropy than the entropy of the pairs themselves, right? So I can know how far away I am from optimal, for an admittedly silly definition of optimal.
Here for the iq image, I’m 110927 bit away, about 13KB or around two tenths of a bit per pixel. So what else is to be done?
The classic transformation, diff[i+0], diff[i+1] -> (diff[i+0] + diff[i+1])/2, (diff[i+0] - diff[i+1])/2 isn’t reversible. Correcting this gives
u8 mid = (data[i+0]>>2) + (data[i+1]>>2) + (data[i+0]&data[i+1]);
u8 a = (data[i+0] < data[i+1]) ? mid : (mid + 0x80);
u8 b = data[i+1] - data[i+0];
data[i+0] = a;
data[i+1] = b;
, which does a bit worse at 6090994, 6930048, 6749589. I tried another of a similar variety,
u8 diff = data[i+1] - data[i+0];
u8 mid = (data[i+0]>>2) + (data[i+1]>>2) + (data[i+0]&data[i+1]);
u8 a = (diff - 0x7f < 0x80) ? mid : (mid + 0x80);
u8 b = data[i+1] - data[i+0];
data[i+0] = a;
data[i+1] = b;
which performs at at 6003654, 6811173, 6615952. This is cool, it’s our first example of something that gives better results only some of the time. I’d show an image of which pixels are the problematic ones that contribute all of the entropy, but it’s obvious that it’s the hard edges.
I was curious about what sorts of mappings I had missed. The mapping data[i+0], data[i+1] -> data[i+0], data[i+0] - data[i+1] is really simple, are there better ones?
I wrote a brute forcer that runs through all invertible linear maps.
double best_entropy = 100000000;
for (int a = 0; a < 256; ++a)
for (int b = 0; b < 256; ++b)
for (int c = 0; c < 256; ++c)
for (int d = 0; d < 256; ++d) {
u8 det = ((u8)a * (u8)d - (u8)c * (u8)b);
if (det%2 == 0) continue;
int histo[256][2] = {0};
for (int i = 0; i < width*height; i += 2) {
u8 out0 = ((u8)a*data[i+0] + (u8)b*data[i+1]);
u8 out1 = ((u8)c*data[i+0] + (u8)d*data[i+1]);
histo[out0][0] += 1;
histo[out1][1] += 1;
}
double entropy_split[2] = {0};
for (int p = 0; p < 2; ++p)
for (int i = 0; i < 256; ++i) {
if (histo[i][p] > 0) entropy_split[p] += histo[i][p] * -log2((double)histo[i][p] / (width*height/2));
}
double entropy = entropy_split[0] + entropy_split[1];
if (entropy < best_entropy) {
best_entropy = entropy;
printf("%f\n", best_entropy);
printf("%d %d %d %d\n", a, b, c, d);
}
}
I let in run for like an hour before realizing I never set -O3, I was just running a debug build. And then a minute later I accidentally killed the process when trying to copy something from the terminal window lmao. It only got to the matrix [ 0 49; 115 141 ] before it was killed, and in that time it found the [ 0 1; 1 -1 ] matrix from before, and a handful of other matrices whose measured entropy was equal to it up to 6 decimal places. I wrote another one that just checks the matrices with with elements between -5 and 5, since higher even multipliers just zero low bits and higher odd multipliers just scramble bits, and the best it found was our friend [ 0 1; 1 -1 ].
I tried writing a more general brute forcer, but all it tried to do is something like this:
[image]
Not very helpful.
Just for shits and giggles, I tried the classic orthogonal square wave decomposition data[i+0], data[i+1] -> data[i+0] + data[i+1], data[i+0] - data[i+1]. It’s not reversible, but who knows? I do, it’s 6090554, 6963846, 6775737, not the greatest.
I tried to come up with an enumeration of all the different kinds of mappings that are continuous, but couldn’t come up with anything usefully different that what I have.
Future TODO:
n pixels, interpolate between them, and then encode the difference.n = 2 case, I predict that most middle pixels either take on values close to the left neighbor, close to their right neighbor, for close to their middle value. Investigate this.Let’s look at quads now. They’re interesting.
So the combinatorics on the size of the histogram for full quads is real real bad. If done like earlier, the histogram would need 2^40 bits. BUT in a 1024x1024 image, there are only 2^18 2x2 pixel quads, coming out to 2^26 bits or 256KB maximum to store them all. A bit much, but it’s good to remember that it’s an option.
I measured the entropy of each image’s quads:
Wow, awesome! These numbers are better than our previously best numbers, the running differences. Of course, this can’t be used as-is because of the histogram storage problem. But our trick of finding a good transformation of the bytes and entropy encoding them separately might do the trick.
Trying
// quad separated 1
for (int i = 0; i < width*height; i += 4) {
data[i+1] = (data[i+1] - data[i]);
data[i+2] = (data[i+2] - data[i]);
data[i+3] = (data[i+3] - data[i]);
}
int histo[256][4] = {0};
for (int i = 0; i < width*height; i += 1) {
histo[data[i]][i%4] += 1;
}
double entropy[4] = {0};
for (int p = 0; p < 4; ++p)
for (int i = 0; i < 256; ++i) {
if (histo[i][p] > 0) entropy[p] += histo[i][p] * -log2((double)histo[i][p] / (width*height/4));
}
printf("entropy: %f %f %f %f = %f\n", entropy[0], entropy[1], entropy[2], entropy[3], entropy[0] + entropy[1] + entropy[2] + entropy[3]);
Disappointing. How about taking one of our known good pair mapping functions and apply them horizontally to both rows, and then vertically to both columns.
for (int y = 0; y < height; y += 2)
for (int x = 0; x < width; x += 2) {
data[(y+0)*width + (x+1)] = (data[(y+0)*width + (x+1)] - data[(y+0)*width + (x+0)]);
data[(y+1)*width + (x+1)] = (data[(y+1)*width + (x+1)] - data[(y+1)*width + (x+0)]);
data[(y+1)*width + (x+0)] = (data[(y+1)*width + (x+0)] - data[(y+0)*width + (x+0)]);
data[(y+1)*width + (x+1)] = (data[(y+1)*width + (x+1)] - data[(y+0)*width + (x+1)]);
}
Okay that’s a little better, but honestly I expected a lot more.
Another way of looking at this last transformation is that the top-right and bottom-left are being encoded according to the pairs-separated method, and the bottom-right is being predicted as the value it would be if the 2x2 pixel block were a smooth gradient.
Let’s see where all of our precious entropy is going:
imgcmp(squiggles_quad_entropy_0.png)quad entropy coef 0[quad entropy coef 1]
imgcmp(squiggles_quad_entropy_2.png)quad entropy coef 2[quad entropy coef 3]
Of course the entropy of coefficient 1 is high on diagonal and vertical edges, coefficient 2 is high on diagonal and horizontal edges, and coefficient 3 is high on diagonal edges.
For that matter, what would happen if I graphed quad entropy per pixel?
img3(iq_quad_entropy.png)quad entropyquad entropy[quad entropy]
Huh. I can’t believe I hadn’t done this yet. Okay, so I guess the strategy for quad entropy is to lean heavily on areas with solid colors. I guess that makes sense.
I suppose that it might make more sense to measure quad entropy relative to the top left pixel.
Remember, these numbers aren’t necessarily compatible to the previous ones because critical information about each quad of pixels have been removed. To get a compatible number you’d have to add 2017449, 1960355, and [TODO] resp. But you get these images:
img3(iq_quad_entropy_rel.png)quad entropy relative to top-leftquad entropy relative to top-left[quad entropy relative to top-left]
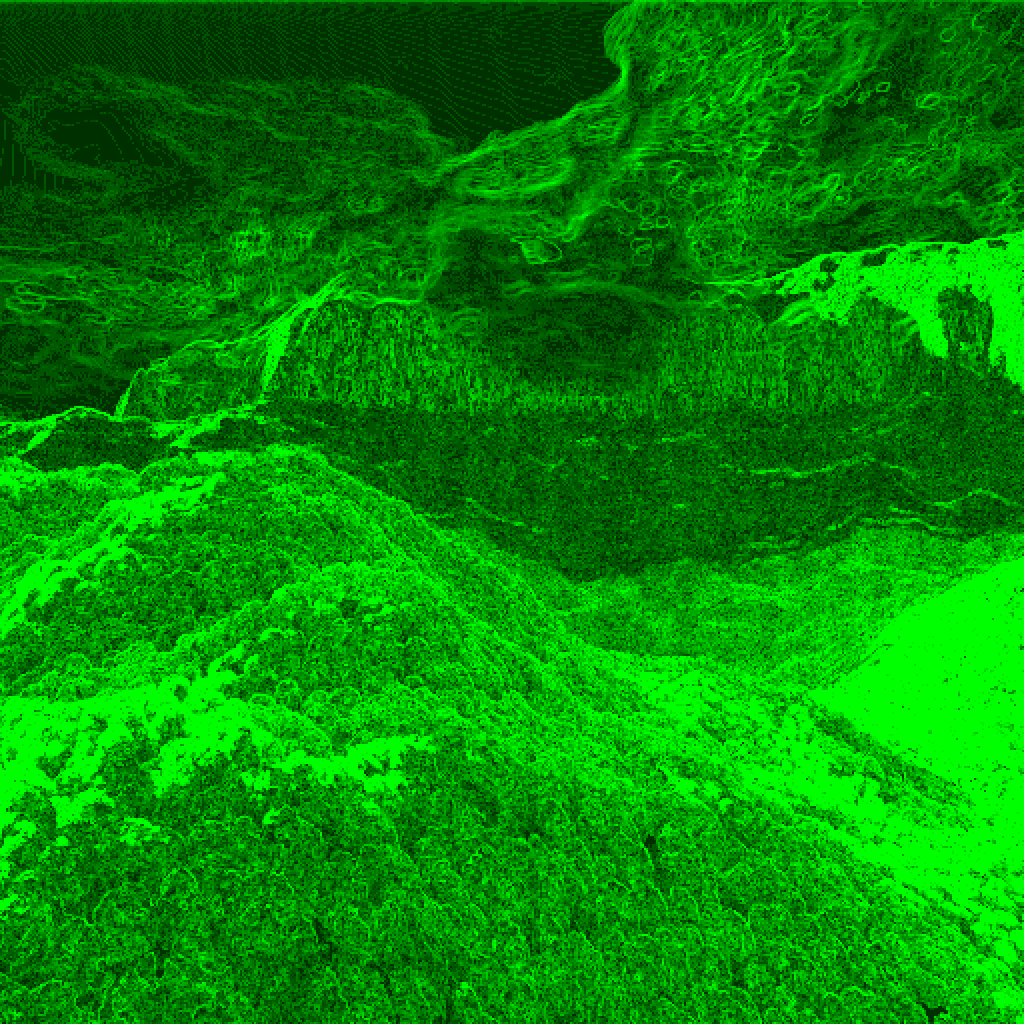All of the brightness scales on these images are the same, measured relative to log2(1024*1024/4) = 18 bits. This last set of images is about what I expected. High values on edges and noise, low values on smooth gradient areas.
I looked at it for a bit and tried some things, and nothing jumped out at me as an obvious transform to try to lower the separated entropy. So I tried the brute force method again. Doing a full brute force of all 4x4 invertible linear maps is far too much to bite off, so I’m only considering maps with coefficients between -1 and 1:
double best_entropy = 100000000;
for (u8 a = 255; a != 2; ++a) for (u8 b = 255; b != 2; ++b)
for (u8 c = 255; c != 2; ++c) for (u8 d = 255; d != 2; ++d)
for (u8 e = 255; e != 2; ++e) for (u8 f = 255; f != 2; ++f)
for (u8 g = 255; g != 2; ++g) for (u8 h = 255; h != 2; ++h)
for (u8 i = 255; i != 2; ++i) for (u8 j = 255; j != 2; ++j)
for (u8 k = 255; k != 2; ++k) for (u8 l = 255; l != 2; ++l)
for (u8 m = 255; m != 2; ++m) for (u8 n = 255; n != 2; ++n)
for (u8 o = 255; o != 2; ++o) for (u8 p = 255; p != 2; ++p) {
u8 det0 = f*k*p + g*l*n + h*j*o - f*l*o - g*j*p - h*k*n;
u8 det1 = e*k*p + g*l*m + h*i*o - e*l*o - g*i*p - h*k*m;
u8 det2 = e*j*p + f*l*m + h*i*n - e*l*n - f*i*p - h*j*m;
u8 det3 = e*j*o + f*k*m + g*i*n - e*k*n - f*i*o - g*j*m;
u8 det = a*det0 - b*det1 + c*det2 - d*det3;
if (det%2 == 0) continue;
int histo[256][4] = {0};
for (int y = 0; y < height; y += 2)
for (int x = 0; x < width; x += 2) {
u8 dat0 = data[(y+0)*width + (x+0)];
u8 dat1 = data[(y+0)*width + (x+1)];
u8 dat2 = data[(y+1)*width + (x+0)];
u8 dat3 = data[(y+1)*width + (x+1)];
u8 out0 = a*dat0 + b*dat1 + c*dat2 + d*dat3;
u8 out1 = e*dat0 + f*dat1 + g*dat2 + h*dat3;
u8 out2 = i*dat0 + j*dat1 + k*dat2 + l*dat3;
u8 out3 = m*dat0 + n*dat1 + o*dat2 + p*dat3;
histo[out0][0] += 1;
histo[out1][1] += 1;
histo[out2][2] += 1;
histo[out3][3] += 1;
}
double entropy_split[4] = {0};
for (int p = 0; p < 4; ++p)
for (int i = 0; i < 256; ++i) {
if (histo[i][p] > 0) entropy_split[p] += histo[i][p] * -log2((double)histo[i][p] / (width*height/4));
}
double entropy = entropy_split[0] + entropy_split[1] + entropy_split[2] + entropy_split[3];
if (entropy < best_entropy) {
best_entropy = entropy;
printf("%f\n", best_entropy);
printf("%d %d %d %d\n", a, b, c, d);
printf("%d %d %d %d\n", e, f, g, h);
printf("%d %d %d %d\n", i, j, k, l);
printf("%d %d %d %d\n\n", m, n, o, p);
}
}
Whew, I hope I did that right. This 2x2 pixel block brute forcer may very well be the biggest one I’ll be able to write. I’m not sure I’ll be able to deal with the 4x4 brute forcer.
The mapping for quad separated 2 is [ 1 0 0 0; 1 -1 0 0; 1 0 -1 0; 1 -1 -1 1 ], and the brute forcer did NOT find a better mapping than that.
Again, the classic square wave decomposition is non-invertible but I’m trying it for shits and giggles:
In preparation for writing a running difference version for pixel quads, like I did for pixel pairs above, I modified the brute forcer to just look at the entropy of the bottom right pixel. And the result is… [ 1 -1 -1 1 ]. I’m not going to write the true running difference transform, I’ll just extrapolate it from the numbers I have here: it should be
Still not quite beating PNG, but a little bit closer now. All three were within 8% of their respective PNG sizes, measured relative the PNG size. In fact, quad running difference squiggles was a mere 800 bytes away! Another interesting thing to note is that for xp_pipes, the transform [ 0 0 1 -1 ] was actually slightly better by about 600 bytes.
But there’s one more thing I’d like to try. In a running difference situation, by the time you get to a pixel for decoding, you’ve already decoded the pixel to the top and to the left. So unlike all the stuff that was happening above, where I was trying to transform pixels in a way that preserves enough info to recover all of the inputs, I can go wild. Any transformation of the form crazy_function(top, left) - curr is fair game.
Specifically I was thinking about the transformation (top + left)/2 - curr. I’m hoping that it’ll be a big win, since
Of course variance isn’t the same as entropy, and divisions by two are lossy, but hopefully it’s enough justification for this method being much better than the first running difference we did!
int histo[256] = {0};
for (int y = 1; y < height; y += 1)
for (int x = 1; x < width; x += 1) {
u8 curr = data[(y+0)*width + (x+0)];
u8 left = data[(y+0)*width + (x-1)];
u8 top = data[(y-1)*width + (x+0)];
u8 out = (left + top)/2 - curr;
histo[out] += 1;
}
double entropy = 0;
for (int i = 0; i < 256; ++i) {
if (histo[i] > 0) entropy += (double)histo[i] * -log2((double)histo[i] / ((width-1)*(height-1)));
}
printf("entropy: %f\n", entropy);
Soooo cloooose! Each is under 2%, and squiggles is just barely under PNG!
Future TODO:
n transformations that do well in mutually exclusive and covering situations, and then find the entropy of the choice between them.I think there are a lot of conclusions that I can draw from this exercise.
First, a blog post in this style is so stupidly long for the actual information contained.
The whole “compute the entropy of the pixel blocks, and use number as a minimum to aim for” is maybe a little silly but can definitely be taken farther than I’m taking it. I suppose I didn’t gain as much intuition about entropy as I would have liked because here at the end I’m looking at the whole pixel block entropies and I’m wondering what those number even means.
Taking mappings that work with low numbers of inputs and applying it to larger numbers of inputs… seems to work? At least so far.
Running differences are so much better than block-based, at least for the moment. The quad running difference isn’t as brain-dead simple to SIMD-ify or GPU-ify as the quad macroblock method, but I guess that’s just the cost I have to pay.
My current best results are sitting between 3.5 and 5 bits per pixel. I guess I feel like it should be way way better than that already. So like 3 bits gets you only 8 possible values. But get this, I measured how much of the pairs entropy came from pairs that are within 4 values (7 possible differences) of each other, and it was 4637169 (out of 5903458 in iq.png, or about 78%). But the number of pixels that that counts is 441742, which brings us to the conclusion that among those small differences the average bits per pixel is 10.5! I guess I didn’t expect the empty parts of the main diagonal to be so costly.